While aberration graphs are great for providing an optical designer with a lens' performance, usually, especially for the user or evaluator of the lens, an objective standard is very much needed.

The modulation transfer function (MTF) is one of the most widely used criteria for the evaluation of incoherent light imaging, where the focus is on image contrast or sharpness.

In fact, many modern optical lenses are directly measured by MTF performance.

As shown in Figure 1, consider an optical system imaging a grating with a sinusoidal intensity distribution. For incoherent light imaging, the intensity of the image is also sinusoidal, but the contrast is reduced.

Figure 1 Object image comparison of an optical system

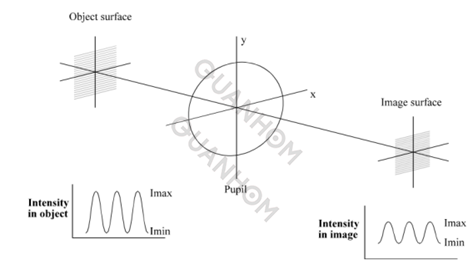
MTF is the contrast of the image divided by the contrast of the object; obviously, it is a function of spatial frequency, and plots of MTF as a function of spatial frequency (usually in "line pairs/mm") are often used in optical design.

The optical transfer function is defined as:

Strictly speaking, we should distinguish between optical transfer function (OTF) and modulation transfer function (MTF).

The OTF is a vector that includes the phase and amplitude of the image, where the amplitude is the MTF.

In fact, the main consideration in optical design is MTF. The phase term, sometimes referred to as the phase transfer function (PTF), represents the deviation of the actual sinusoidal image from the ideal sinusoidal image, expressed as a function of the phase angle as a function of spatial frequency. If the phase exceeds 180°, the MTF may be negative. This represents a phase reversal, which results in a reversal of the contrast of the image. In reality, this can happen at the high frequencies of many lenses.

1. Theory

For systems illuminated by incoherent light, the MTF can be obtained using the Fourier transform of the line spread function. Usually, MTF is obtained in this way.

However, the diffraction OTF can be quickly solved using autocorrelation integration:

where D(s)=OTF, A=light pupil area, S is the overlapping area of the two light pupils, W is the wavefront aberration, S is the simplified spatial frequency equal to fλ/NA, and NA is the numerical aperture.

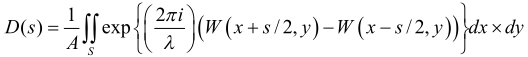
2. Geometric approximation

In the geometrical optics approximation, we assume that λ is close to zero, so the MTF (in the Meridional direction) is:

This is the integration of the whole pupil, which in practice can be approximated by a simple summation.

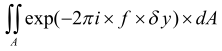
3. The actual solutionBecause we need to know not only the sagittal direction but also the MTF in the meridional direction, the MTF in the sagittal direction is solved by the following formula:

The MTF in the meridian direction is obtained by the following formula:

It is convenient to trace numerous (often more than 100) rays of light, but only the rays that actually pass through the system are considered for the summation calculation. We also trace rays of multiple wavelengths, and the wavelengths can be weighted differently when summing. It is easy to add a correction factor to the geometric MTF by multiplying the geometric MTF by the diffraction MTF of the ideal system. Such a result allows the geometric MTF to be accurate in both large aberration systems and small aberration systems.

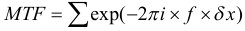
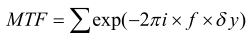
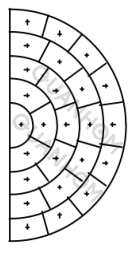
However, for moderate aberrations, geometric MTF usually gives disappointing results. Now, we have to decide how many ring rays to trace. Taking the rays in the way shown in Figure 2, it can be seen that the areas of all small area in the semicircle are equal. It is easy to see that if there are n rings of rays, the total number of rays is 2n. When the optical system is symmetric (symmetric about the meridian y plane), to save time, the program does not need to calculate rays in the negative x direction.

Figure 2. Line-taking method for calculating geometric MTF

4. Diffraction limitWhen a lens with a finite pupil aperture forms images of a sinusoidal object, the limiting frequency of its diffraction MTF is:

For example, for an f/2 lens with a numerical aperture NA of 0.25, when the wavelength λ is 0.0005 mm, the cutoff frequency is:

This frequency corresponds to a grating with a spatial period of 0.001 mm (1μm), but note that the MTF value corresponding to this frequency is zero. For 500 / cycles mm, the MTF of an ideal lens is about 40%, so f/2 is a more realistic frequency.

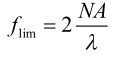
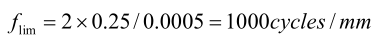
5. MTF in ZEMAXThe MTF used in ZEMAX functions both as an evaluation tool and as an optimization tool.

In the above figure, there are totally four curves, of which two are meridional MTF curves, and the other two are sagittal MTF curves. In the 0°field of view, the meridional MTF curve and the sagittal MTF curve are coincident; and in the 2°field of view, the meridional MTF curve and the sagittal MTF curve are quite different. This is because the PSF becomes asymmetric when it is off axis, resulting in a difference in the width and profile of the PSF along with the meridional and sagittal directions. Thus, convolving with the paraxial (or geometric) image will result in a delta in both directions. This also means that the resolution is different in these two directions.

The above briefly describes the method of judging the performance of optical lenses. 

QUANHOM is a custom optical lens manufacturer. Our team bridges the gap between superior performance and limited budget, especially when we are involved in projects integrating high precision. Products include infrared optical assemblies for VIS/SWIR/MWIR/LWIR, eyepieces, infrared lens elements (from monoscopic to Quickly switching between multi-field and continuous zoom infrared lenses), etc. Our experienced and inspired experts are always able to provide optimized IR lens glass, and optomechanical, and optoelectronic assembly options.