Fast Focal Length Measurement Method based on Infrared Lens Images
The focal length of the lens refers to the distance from the principal point to the focal point of the lens optics and is an important performance index of the lens. The length of the lens focal length determines the size of the image taken, the size of the field of view, the size of the depth of field, and the perspective of the picture. Therefore, how to accurately detect the focal length of an infrared lens is an important research content of infrared lens parameter detection.
The method of infrared lens focal length measurement can be divided into the direct method and the indirect method. The indirect method is to reversely derive the focal length of the lens by measuring the angle of view of the lens. However, the premise of the indirect method is that there is no lens distortion.
In the actual measurement, especially for small focal length lenses, the distortion is not negligible, which leads to the inaccuracy of the lens focal length calculated by the indirect method; the direct method is to obtain the target image information, then get the focal length of the lens.
The current mainstream equipment is lens MTF measurement equipment. This equipment has high measurement accuracy and good consistency, but the equipment is expensive, the lens focal length measurement cost is high, and the efficiency is low, which is not conducive to the rapid detection of batch lenses.
Aiming at the current situation, this paper proposes a fast detection method of infrared lens focal length based on the knife-edge target image. This method collects the image of the knife-edge target in the focused state of the infrared lens, uses the Otsu threshold segmentation method to obtain the binarized image, and extracts the edge contour of the target, and then uses the affine transformation to obtain the minimum circumscribed rectangle corresponding to the knife-edge target, and the circumscribed rectangle.
The vertex coordinates are brought into the focal length calculation formula, and then the corresponding focal length of the infrared lens is estimated. The method can realize the rapid and accurate measurement of the focal length of the infrared lens in batches, and can effectively reduce the cost of lens parameter measurement.
1. Theory and Method
1.1 Adaptive threshold segmentation
The maximum between-class variance method (Otsu) is a general detection and segmentation algorithm. In view of the situation that the double peaks of the image gray histogram have no obvious troughs or the double peaks and troughs are not obvious, the maximum between-class variance method is suitable to determine the segmentation threshold position between the double peaks.
This method uses the zero-order and first-order cumulative moments of the image gray histogram to maximize the discriminant function to select the best threshold for image segmentation.


1.2 Edge extraction
Edge extraction is a common method for segmenting images based on pixel gray mutations. Commonly used edge extraction methods include the morphological gradient-based edge extraction method, Sobel edge extraction method, Laplacian edge extraction method, and Canny edge extraction method.
The method of edge extraction based on the morphological gradient is to subtract the result of morphological expansion from the result of morphological corrosion in the image to obtain the edge contour information containing the target gradient. This operation will change the pixel size of the target after imaging and affect the calculation accuracy.
The Sobel edge extraction method and Laplacian edge extraction method have low edge extraction accuracy when the convolution kernel is small. For larger convolution kernels, more pixels are used in the approximation process, so the time loss is large.
This article chooses the Canny edge extraction method. This method first calculates the first-order derivatives in the x and y directions, and then combines them into 4 directional derivatives, and combines the local maximum points in the directional derivatives to form edge candidate pixels.
Finally, when extracting the edge contour, the Canny method uses two thresholds. If the pixel gradient is greater than the larger threshold, it is marked as a valid edge; if the pixel gradient is less than the smaller threshold, it is marked as an ineffective edge; if the pixel gradient is between Between the two, only when it is connected to a high-threshold pixel, is it marked as a valid edge.
1.3 Affine transformation
Affine transformation is an important processing method in image geometric transformation. It maps any parallelogram ABCD in the plane to any other parallelogram ABCD and maintains the straightness and parallelism of the line segments before and after the transformation.
Through the affine transformation, geometric transformations such as translation, rotation, expansion, and reversal of the image can be realized. The affine transformation on the two-dimensional Euclidean space can be expressed as formula (1). According to formula (1), the typical affine transformation mainly has the following types:
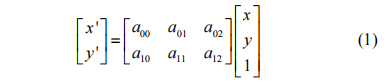
(1) Translational transformation. Move the point (x, y) to the point (x + a, y + b), then the change matrix is:
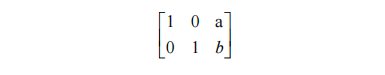
(2) Scaling and transformation. If the horizontal coordinate of the point (x, y) is enlarged or reduced by times, and the ordinate is enlarged or reduced by b times, the transformation matrix is:
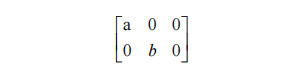
(3) Rotation transformation. Rotate the target graphic counterclockwise in radians around the origin, then the transformation matrix is:

1.4 Derivation of focal length calculation formula
The schematic diagram of the rectangular target through the optical imaging system is shown in Figure 1.

Fig.1 Schematic diagram of the target image by the optical system
Where x_target is the physical width of the rectangular target, and y_target is the physical height of the rectangular target, both in mm. The size of the output image of the rectangular target after being imaged by the optical system is m×n, and the pixel size of the target in the image is q-p and s-r, and the units are all pixels. Using the triangular relationship of the optical imaging system, the following relationship can be obtained:
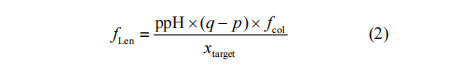
Where: ppH is the horizontal size of the detector, μm; fcol is the focal length of the collimator tube, mm; flen is the focal length of the infrared lens, mm. The relationship between the instantaneous horizontal field of view of the detector and the focal length of the lens is as follows:

Therefore, the focal length of the infrared lens:

Among them, substituting equation (2) into equation (3), the instantaneous horizontal field of view angle of the detector can be obtained:
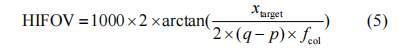
2. Experimental results and analysis
The target selected in this paper is a knife-edge target with a radius of 16 mm, a collimator focal length of 260 mm, an uncooled detector with a resolution of 640×512, a pixel spacing of 17μm, and the theoretical focal length of the infrared lens is 54 mm.
Figure 2(a) is the output image of the knife-edge target through the optical imaging system when the infrared lens is in the focused state, Figure 2(b) is the result of the target edge extraction after the image is binarized, and Figure 2(c) is the target simulation The output result after radiographic transformation. It can be obtained from Figure 2(b) that the method can accurately extract the edge contour of the knife-edge target.
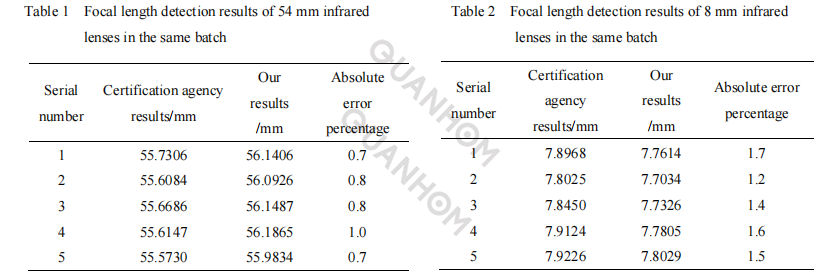
Bringing the coordinates of the vertices of the circumscribed rectangle of the knife-edge target in Figure 2(c) into the calculation formulas (4) and (5), the actual focal length of the 54 mm infrared lens can be obtained as 56.1406 mm, and the focal length of the lens has been tested by the certification body. It is 55.7360 mm, the absolute error is 0.4046 mm, and the error percentage is 0.7.

(a) The original image (b) Image after edge extraction (c) Image after radiation transformed
Fig.2 The processing flow chart of the knife-edge target image
In order to verify the universality of the algorithm in this paper, the focal lengths of 5 infrared lenses of 54 mm and 8 mm in the same batch were calculated respectively, and compared with the test results of the certification body, as shown in Table 1 and Table 2. Combining formulas (4) and (5), the parameters that affect the accuracy of infrared lens focal length measurement include the horizontal size of the detector pixel, the collimator focal length, the physical size of the rectangular target, and the horizontal pixels occupied by the target in the image.
Among them, the horizontal size of the detector pixel, the focal length of the collimator, and the physical size of the rectangular target are affected by the machining accuracy of the machined parts, and there are certain errors, so the entire detection platform needs to be calibrated. The accuracy of the calculated value of the horizontal pixels occupied by the target in the image is related to the focal length of the measuring lens.
An infrared lens with a large focal length has a high image resolution, and the estimated error has little effect on the result, while an infrared lens with a small focal length The resolution of the image formed by the lens is low, and the error of the estimation has a great influence on the result.
Therefore, when calculating the horizontal pixels occupied by the target in the image, it is necessary to perform sub-pixel processing on the image to reduce the estimation error, improve the estimation accuracy of the value, and thereby improve the focal length measurement accuracy. How to improve the measurement accuracy of the infrared lens focal length will be the next step of the research team.
3. Conclusion
This article introduces an image-based rapid detection method of infrared lens focal length. The comparison result shows that the average absolute error percentage of the lens focal length estimated by this method is less than 1.48 relative to the focal length detection result of the certification body. The validity and accuracy of the method are confirmed, and the foundation is laid for the rapid detection of important parameters of the lens.
Quanhom continues to research and develop new detection technologies, and accurately evaluate and improve the performance of infrared optical lenses. We can not only provide users with high-quality products but also formulate thoughtful solutions based on users' actual needs.
As an experienced manufacturer of Opto-electromechanical components, Quanhom is committed to providing users with a variety of thermal infrared cameras (LWIR, MWIR, and SWIR) of excellent quality. We have a good reputation in the industry by virtue of leading R&D technology and excellent manufacturing technology. And our products are sold all over the world and have received praise and trust from many customers. If you want to learn more about our related services, you can send us your needs, and we will give you a satisfactory answer as soon as possible.
Authors: Zhong Jianbo, Li Maozhong, Xia Qingsong, Luo Yongfang, Jia Yuchao, Wang Caiping, Li Hongbing, Luo Hong, Huang Pan
Journal Source: Infrared Technology, Infrared Technology, June 2021
Received date: 2019-04-30; revised date: 2021-06-10.
References:
[1] 许士文. 红外成像系统测试与评价[M]. 北京: 红外与激光工程, 2008: 150-180.
[2] Ohtsu N. A threshold selection method from gray-level histograms[J].IEEE Transactions on Systems Man & Cybernetics, 1979, 9(1): 62-66.
[3] Imocha Singh, Tejmani Sinam. Local contrast and mean-based thresholding technique in image binarization[J]. International Journal of Computer Applications, 2012, 51(6): 5-10.
[4] 赵文涛, 曹昕鸷, 田志勇. 基于自适应阈值区域生长的红外舰船目标分割方法[J]. 红外技术, 2018, 40(2): 158-163. ZHAO Wentao, CAO Xinzhi, TIAN Zhiyong. An infrared ship target segmentation method based on adaptive threshold region growth[J]. Infrared Technology, 2018, 40(2): 158-163.
[5] 郝争辉, 张学松, 王高, 等. 基于边缘轮廓线提取的自动对焦评价函数[J]. 红外技术, 2018, 40(2): 170-175. HAO Zhenghui, ZHANG Xuesong, WANG Gao, et al. Autofocusing evaluation function based on edge contour extraction[J]. Infrared Technology, 2018, 40(2): 170-175.
[6] Gábor Domokos, Zsolt Lángi, Márk Mezei. A shape evolution model under affine transformations[J/OL][2017-09-18]. arXiv:1604.07630 (https://arxiv.org/ abs/1604.07630v2).

